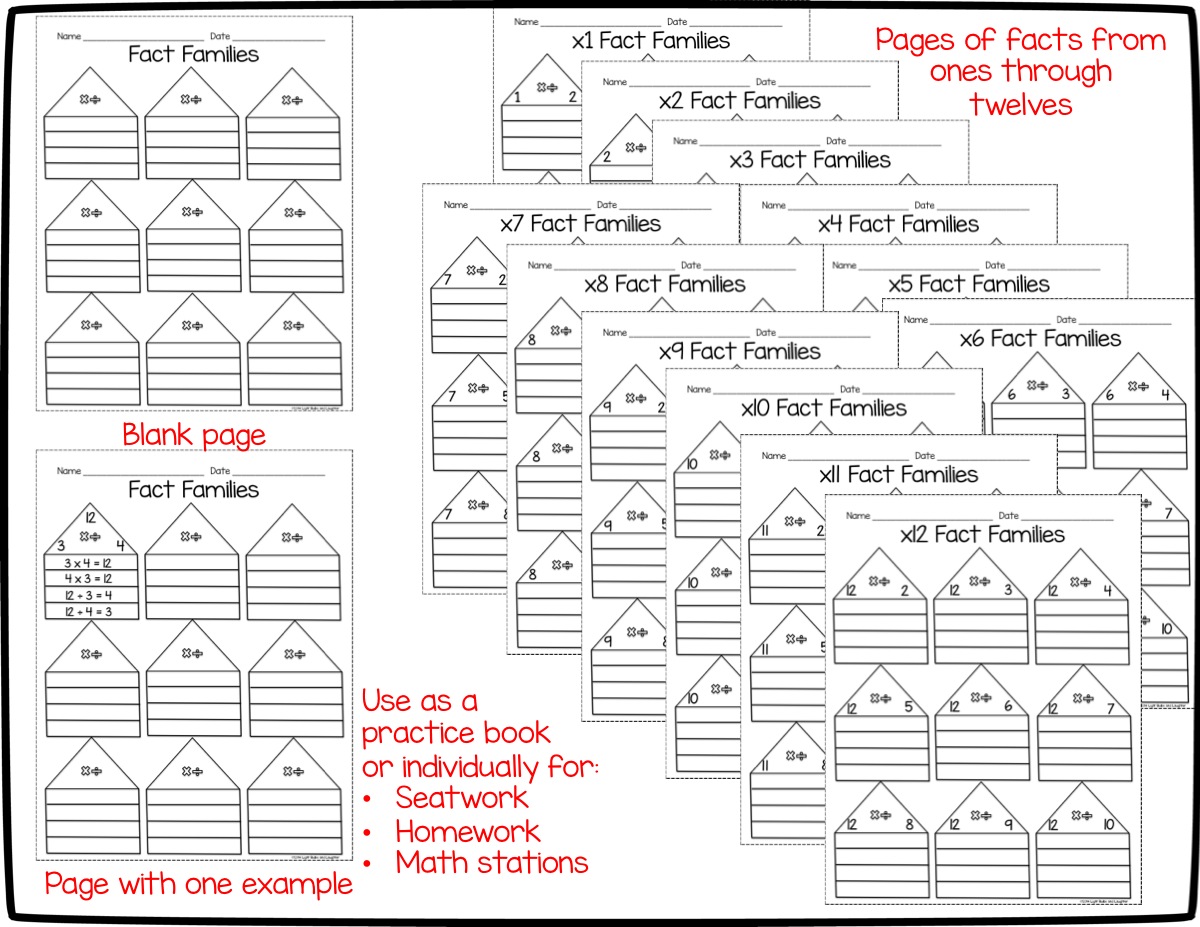
My third graders have been working on multiplication and division for months! First, we focused on understanding what multiplication is. After the conceptual understanding was in place, we began to memorize our facts so that we can use them with fluency. (For my blog post about this, click HERE.)
We have now moved on to division in our lessons, but will continue to do timed tests and memorization for a few more weeks. About a third of the class has completed their ice cream sundaes (See the picture below; they have memorized their facts through the twelves), and moved on to division timed tests.
Yesterday, one of my students came to me before the timed test and said, "I don't know how to do the division threes." She had just passed the ones and twos, but was completely convinced that she did not know the answer to the threes. (Remember, she had learned ALL of her multiplication facts through the twelves!)
We were in our first week back from Christmas vacation, during which each student completed review homework that looked like this (including a page for each set of fact families from the ones through the twelves):
We went to check her homework, and she had completed the whole thing. Perfectly. All twelve pages. We talked about the idea that if you know your multiplication facts, you know your division facts, also. This is because they are in the same fact family. I could not get her to believe me until I showed her the division sentences that she had written! Her "light bulb moment" was a joy to see. Her smile lit up the room when she realized that she already knew every answer.
Sometimes I assume that students understand the big picture behind something, because they are able to do the specific task that I assign. But how do I know for sure? I guess I actually have to talk to them. Individually. If she hadn't approached me to let me know her dilemma, I would not have known there was a problem. It's also possible that they might forget what something means. After all, I forget things all the time!! (Where did I put my keys?)
I'm a little embarrassed to admit all of this... sometimes I focus so much on the students who are obviously struggling that I don't see what's happening with my "on grade level" kids. When I pull a small group to work with, these kids are usually not part of it. So here's a resolution for the new year: I will try to meet with each student individually, once per week, to talk about where they are in their math journey. (It seems much easier to do this for language arts, between reading with students and doing fluency testing, etc.)
This week, I plan to show each student their completed fact family practice book and ask for an explanation of how it works. It should be interesting!
If you are interested in my Multiplication and Division Fact Family Practice Pack, you can find it in my TpT store.
Happy Teaching with Fact Families,
Word problems are a HUGE part of teaching elementary math! The best way that I have found to get students excited about word problems is to have them write their own. When it comes to addition and subtraction, my third graders do pretty well.
First, we work together as a class. I choose a student to help me. This students gets to say where we are going (Walmart is a favorite), and what we are purchasing (video games and candy top the list). They decide what each item costs, and we put it together like this:
Ana went to _____________. She bought one _________ for $_____ and two ___________s for $_______.
Next, we decide whether we want to add or subtract. If we add, the final sentence would be something like, "How much did Ana spend altogether?"
If we subtract, we might use the sentence, "How much more did the ________ cost than the _______?"
Finally, I have the students do the problem on white boards, either individually or in groups, and we discuss our answers. When we have mastered this, I have students write their own word problem and share it with a partner who must solve it.
Multiplication word problems should be easy after this, right? Well. Sort of. We had a bit of a problem with this earlier in the year. I started us off with the idea of rows of desks. I chose a student who decided how many rows, and how many desks in each row. Easy. We followed the same pattern of working whole class, then working with partners.
This is when things got tricky. See, I did what I always do. I changed the lesson in the middle. It seemed like a great idea to leave one of the numbers out of the equation and ask this question: "How many days are there in eight weeks?" Instead of answers, I got a lot of blank stares. Then I tried, "How many horseshoes do I need for nine horses?" This time they did a little better.
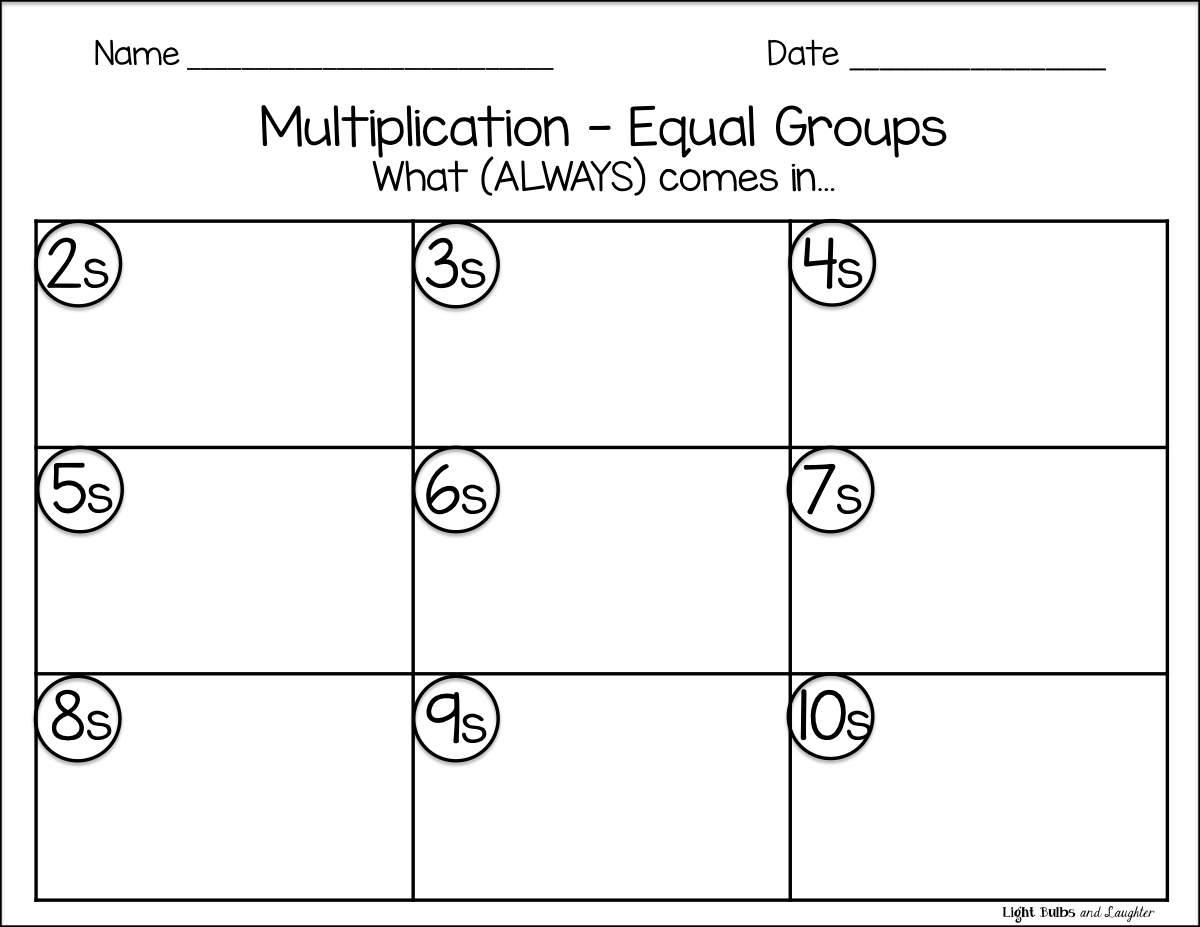
What I realized is this. My students were so used to being given two numbers to multiply that they couldn't seem to think beyond this to figure out one of the numbers for themselves. So I got a large sheet of paper and made a 3x3 grid. I labeled each box with the numbers from two through ten. And I asked my students, "What comes in twos?"
I was shocked by their answers, which were as follows: desks, candy bars, apples, and books. What?! I tried again, putting emphasis on a particular word. "No, what COMES in twos?" They continued to give me answers such as pencils, rulers, magnets, and desks. I was stumped. Then I realized what was happening. They were so used to making groups of objects to multiply that in their minds anything could come in groups of any number. I was not asking the right question!
I tried again, adding the word ALWAYS, and gave them a clue. "What always comes in groups of two? Think about your brains." I pointed to my head and watched the understanding dawn on their faces as most of them raised their hands to answer the question, "Hemispheres!" (We talk about our brains a lot.) Of course I had to ask for a complete sentence, and we finally heard, "Hemispheres always come in groups of two!" Whew.
Now we were cooking with gas. We started filling up the chart with things that always come in groups of a particular number. Some were a lot more difficult than others! Here's a picture of our (not terribly attractive) chart.
We didn't do very well with some of the numbers, so I added more later! I have to mention two particular students here. The first just wasn't understanding, and kept blurting "desks!" every time I asked, "What always comes in..." The second student questioned most of the answers with words like these, "What if you accidentally cut off your finger?" and "What if I step on the spider and half his legs fall off?" Arrrgh.
Somehow we made it through our lesson, and I think that we are better for it. We did some good thinking about numbers and groups and multiplication, and we had a lively debate about changing the word always to usually, because of the potential to cut our fingers off and step on spiders - to which I say, ick. (My word, always, won the debate. This is one of the perks of being the teacher.)
So. If you would like to have your students think about what (ALWAYS) comes in groups, I have a freebie for you. Well, two, actually. In case you would rather have the numbers spelled out. Click on any picture in the post to go to my TpT store for the free download.
Happy Multiplication Word Problems,